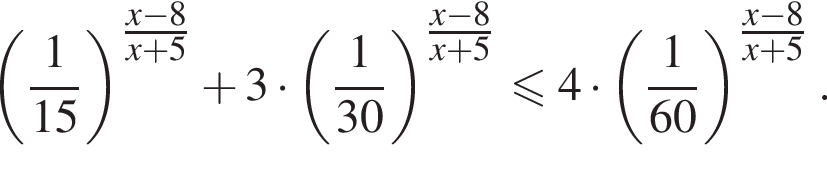
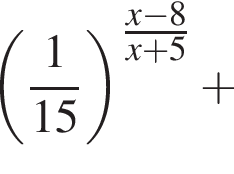
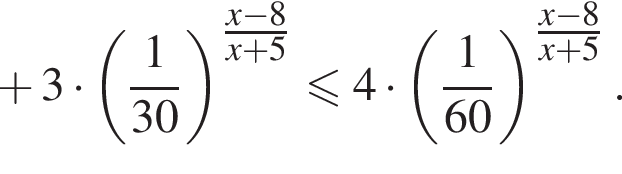
Ре­ше­ние. Пусть 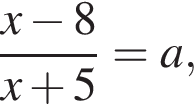тогда

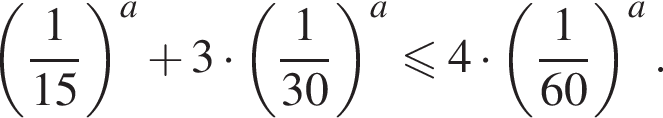
Раз­де­лим обе части не­ра­вен­ства на 30^a > 0, по­лу­чим:

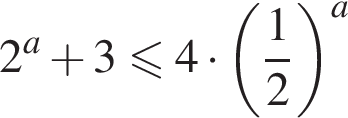
За­ме­тим, что левая часть мо­но­тон­но воз­рас­та­ем на всей об­ла­сти опре­де­ле­ния, а пра­вая мо­но­тон­но убы­ва­ет. Сле­до­ва­тель­но, при a  =  0 левая и пра­вая части не­ра­вен­ства равны, зна­чит, не­ра­вен­ство верно при Тогда

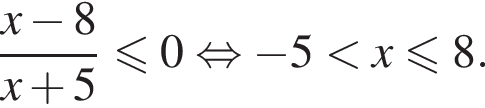
Наи­мень­шее целое ре­ше­ние равно −4, а ко­ли­че­ство всех целых ре­ше­ний не­ра­вен­ства  — 13. Про­из­ве­де­ние наи­мень­ше­го це­ло­го ре­ше­ния на ко­ли­че­ство всех целых ре­ше­ний не­ра­вен­ства равно −52.

Ответ: −52.